Localiser un robot mobile dans un environnement virtuel grâce a la programmation par contraintes.
Dans l’article précédent, j’ai présenté rapidement la programmation par contrainte avec beaucoup de texte et un exemple concret. Dans celui-ci, je présente une implémentation d’un SLAM (Simultaneous Localization And Mapping), chargé de localiser un robot mobile dans un environnement virtuel.
Dans cet exemple, on considère que la position du robot a t0 est connue, ainsi que les informations de ses capteurs, comme sa vitesse et son orientation. Durant son périple dans le monde virtuel, notre robot utilisera un LIDAR (également simulé) qui lui donne accès à la distance et l’orientation absolue a des marqueurs de position inconnue. On considère aussi qu’on sait quel marqueur a été remarqué.
Toutes ces mesures ont bien sûr une marge d’erreur que l’on considère connue (dans le monde réel, ces informations sont obtenues d’après la documentation des capteurs utilisés). Cependant, dans notre petit monde virtuel, on exclut totalement l’apparition d’outliers dans les données.
Cette implémentation ne peut pas fonctionner en l’état dans le monde vrai de la vie réelle.
Pour ce projet, j’ai utilisé Tubex, une librairie pour C++/Python de PPC, proposant des outils pour estimer des trajectoires contraintes. Mon implémentation est une amélioration de l’exemple final du tuto (Range Only SLAM).
Pour estimer les performances de notre SLAM, nous allons définir un point de comparaison initial : l’estimation de trajectoire par dead reckoning, “Navigation a l’estime” (???) en bon François, d’après Wikipédia. Le dead reckoning consiste à estimer la trajectoire via une intégration directe de la valeur de ses capteurs. C’est une solution très simple, mais qui a le désavantage d’accumuler rapidement les erreurs avec le temps.
Tubex représente l’incertitude des trajectoires en utilisant des tubes, affichés par un gradient de couleur.
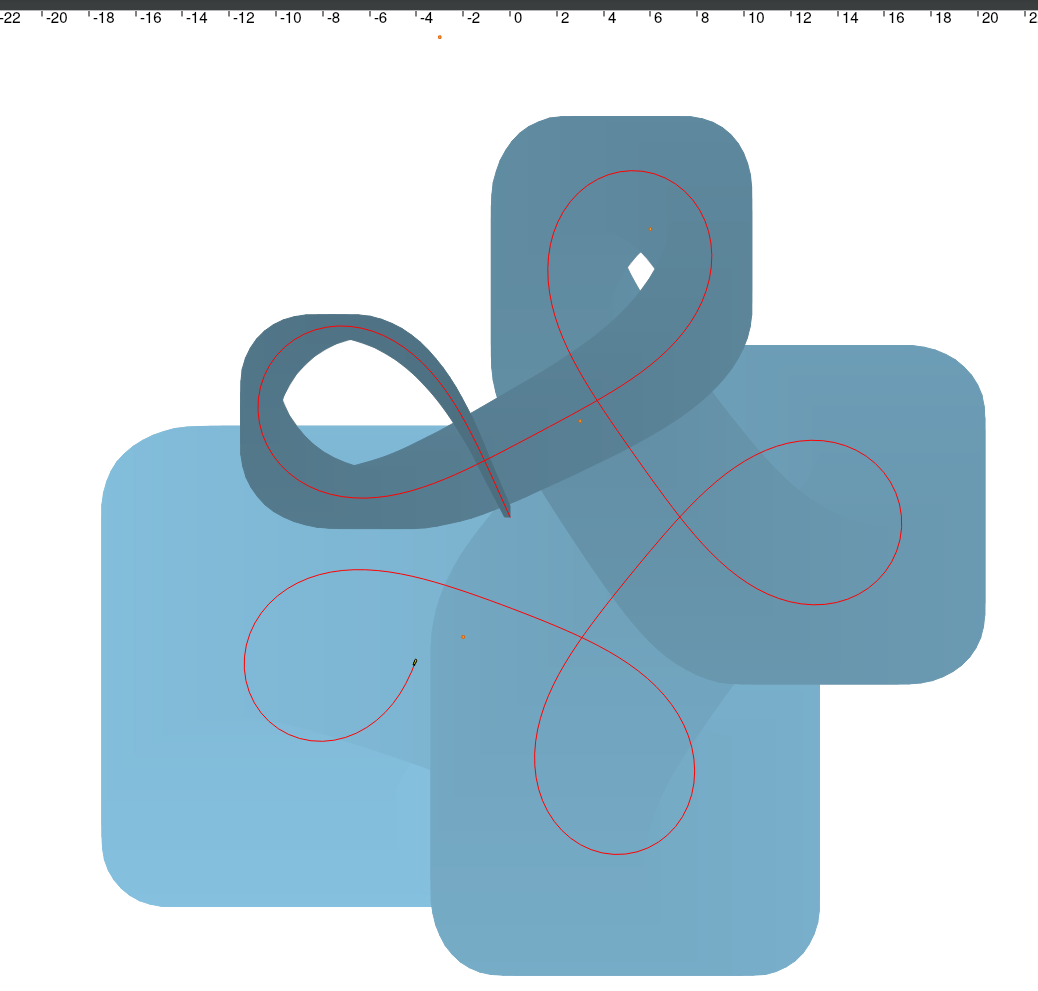
Sur l’image ci-dessus, on peut voir le la trajectoire réelle du robot en rouge, et sa trajectoire estimée via dead reckoning en gradients de bleu. L’incertitude de la position du robot augmente avec le temps, d’où l’élargissement de la trajectoire en bleu, jusqu’à atteindre la position finale, dans un interval de 18x18 mètres. Son point de départ est l’endroit avec le moins d’incertitude, ou la trajectoire bleue est la plus resserrée. Malgré ce manque de précision, la trajectoire réelle ne se retrouve jamais en dehors de la trajectoire estimée.
Les quatre marqueurs de la map sont représentés en orange, et leur position est inconnue.
Cette trajectoire est notre variable de départ, qui sera contrainte par le programme en fonction des observations de marqueurs.
Une V1
Allez, on saute au résultat directement :

Bon alors, qu’est-ce qu’on voit sur cette image ? La partie grisée est l’estimation dead reckoning, qui a été réduite jusqu’à la partie bleutée. On remarque tout de suite que la position estimée du robot est bien meilleure qu’avant : on est dans un interval d’environ 2x1 mètres, ce qui représente une amélioration de l’aire finale de 99.38%.
On observe également des rectangles autour des marqueurs, qui représentent l’estimation de la position des marqueurs par le robot à la fin du processus de mapping. Tout comme le robot, leur position finale est située par un interval.
Une V2 !
Bon, le résultat de la V1 est bien beau, mais en fait, c’est un système assez peu utile : Notre robot est déjà arrivé au bout de sa trajectoire quand on fait l’estimation de sa position. Une implémentation plus utile serait d’obtenir la position du robot à chaque instant t, et c’est ce que nous allons faire.
Notre code n’a pas besoin de beaucoup de modifications pour ça : nous avons seulement besoin d’obtenir la position (et donc réduire les variables) plus régulièrement que juste une fois à la fin.

Cette fois-ci la trajectoire dead reckoning n’est pas modifiée, et est juste affichée pour comparaison. La position du robot a chaque instant t est représentée par un interval en noir.
L’estimation de position instantanée sera de moins bonne qualité que la V1, car on à pas accès tout de suite à l’ensemble des données. Cependant, une fois arrivé au point final, la trajectoire finale sera “contractée” en prenant en compte toutes les données précédentes, et on reviendra au même cas que la V1.