Partie 1: Blabla et implémentation
Je suis nul aux échecs, aux dames, me fait rouler dessus au Puissance 4, bref les jeux de société ne sont pas mon fort. Par contre, je me débrouille pas mal en programmation.
Petite précision : à partir d’ici quand je dis “suite de coups” je parle d’un ordre de jeux : je joue, puis mon adversaire, puis moi etc
Faire un petit saut au-dessus du blabla jusqu’à la partie intéressante.
Imaginez-vous en train de jouer aux échecs
Quelle stratégie adopter ? On peut se dire qu’on va faire au plus simple, et jouer des pions au hasard, mais la probabilité de gagner est assez faible si votre adversaire n’a pas la même stratégie (à part si vous faites semblant de savoir ce que vous faites, ce qui peut le déstabiliser). On va l’appeler la “méthode hasard”.
L’étape au-dessus serait de choisir des coups au hasard complet et garder le meilleur en tête jusqu’à ce que votre adversaire vous annonce “que bon ça fait une heure que tu n’as pas bougé ton pion, je me casse” (victoire !) ou si vous jouez avec un sablier, votre défaite. Cette approche est bien meilleure que jouer directement des coups au hasard, votre solution finale dépend de tous les coups précédents. Il se trouve cependant que dans ce type de jeux, le nombre de coups possibles augmente exponentiellement, impossible de tous les essayer (enfin, possible mais pas sous la pression du sablier !). On l’appellera “méthode exploration”.
Ou alors une autre méthode serait de réfléchir uniquement aux meilleurs coups que vous pouvez faire, puis les meilleurs coups que vous pouvez faire après ces meilleurs coups yadi yada… Ce genre de méthode est qualifiée de greedy (gloutonne), c’est-à-dire qu’elle prend ses décisions sur l’instant, pas le temps de réfléchir a la suite des évènements ! Cette approche est déjà meilleure que les deux précédentes, car on explore moins de possibilités (moins de mal de tête !) et on effectue sont une suite d’actions forcément positives (pour un résultat pas forcément aussi positif). Son désavantage est de tomber facilement dans les minimums locaux, comme se jeter sur un cavalier avec votre dame pour se la faire piquer par un pion. De même, elle ne sacrifiera jamais un pion pour en manger un autre plus dangereux, et sa stratégie est donc très prévisible. On va appeler celle-ci “méthode greedy”.
Ce qu’il nous faut, c’est une méthode capable de rassembler les forces de ses copines, une espèce de Captain Planet des jeux de société ! Heureusement, ce problème a été beaucoup retourné par des gens intelligents (et/ou payez pour ça), qui nous ont trouvé un ensemble de solutions toutes plus originales les une que les autres. Mais ici, on ne fait pas dans l’originalité et on ne va parler que d’arbres, na !
Construire un arbre
Si vous avez déjà touché à l’orienté objet un jour, il est probable que ce genre d’exercice vous soit déjà tombé dessus. Un arbre est une structure de donnée assez basique, ou on a un ensemble de nœuds qui appartiennent à un parent, et ont eu même des enfants qui ont des enfants, etc. C’est une représentation assez intuitive pour nous, pauvre singes, et on la retrouve partout, dans tous les domaines d’application (voir mon petit post sur la génération de galaxies procédurales, ou la galaxie est créée dans un arbre).
Ici, notre racine va être la position de base du plateau, sans aucuns mouvements si je commence, ou avec un mouvement de l’adversaire s’il commence (moins de coups à calculer yes !). Chaque possibilité de jeux depuis la situation initiale va représenter un nouvel enfant pour notre racine. Puis une fois qu’on a exploré tous nos mouvements, c’est le tour de l’adversaire. On génère ses mouvements possibles depuis chacun de nos mouvements, puis c’est mon tour, et ainsi de suite jusqu’à ce qu’on atteigne la fin de la partie (gagné, perdu, égalité, que sais-je).
Petit exemple avec le TicTacToe :
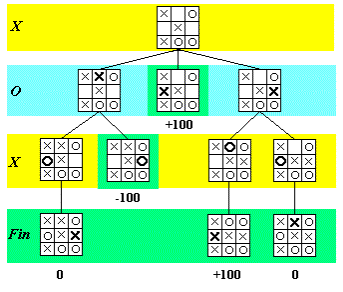 (Emprunté au site turing.cs, à visiter pour des explications d’algorithmes plus variés)
(Emprunté au site turing.cs, à visiter pour des explications d’algorithmes plus variés)
Bien, on a un arbre maintenant.
Exploration avec Monte Carlo
L’arbre qu’on vient de construire est de taille raisonnable pour un tictactoe, ou le nombre de possibilités est réduite. Pour un Puissance 4 ça pourrait encore fonctionner, mais pour les échecs (ou le Go) ça n’est pas viable. Il existe plusieurs techniques pour améliorer tout ça, celle qui nous intéresse s’appelle MCTS “Recherche Arborescente Monte-Carlo” (voir la page Wikipedia, qui bavarde moins que moi).
Cette technique a été utilisée comme la base pour l’algorithme AlphaGo, champion du monde du jeu de Go en 2015 (ptit coup de vieux). Elle se base sur quelques euristiques pour trouver une balance entre exploration de nouvelles possibilités et recherche autour des meilleures suites d’action déjà trouvées. Cela permet de n’explorer qu’une fraction des possibilités tout en trouvant des coups intéressants.
Le but de ce billet de blog n’est pas de faire un historique ou d’expliquer une énième fois cette méthode sur internet, mais proposer quelques modifications
Un petit résumé vite fait pour être sur la même page : le dur de la technique est constitué de 4 étapes :
- Se balader dans l’arbre avec des euristiques jusqu’à atteindre une feuille (un nœud sans enfants).
- Lui créer des enfants : en gros lui ajouter en enfant tous les coups possibles à partir de ce nœud
- Jouer des coups au hasard depuis l’enfant crée juste avant jusqu’à atteindre un état final.
- Faire remonter le score final depuis l’enfant jusqu’à la racine.
Représenter ça en code
On va faire une classe générique très simple pour l’arbre, qui sera responsable de choisir les coups possibles, les dérouler jusqu’à la fin et propager le résultat. Le but n’est pas de donner du code, mais simplement la structure globale et le détail de quelques méthodes.
Interface Game State
Nous allons avoir besoin de coder la logique du jeu. Pour cela, libre à vous de faire ce que vous voulez ! Il y a pour seule contrainte que votre classe de logique hérite de notre interface ci-dessous :
//Interface
class IGame_State {
//renvoi le score de cet etat
virtual double get_score () = 0;
//renvoi le nombre de coups possible depuis cet etat
virtual int get_move_count () = 0;
//effectue un mouvement depuis cet etat et le renvoi
virtual IGame_State* do_move(unsigned int index) = 0;
}
Notre classe dérivée IGame_State sera utilisée dans notre arbre pour savoir où on en est dans la partie.
Elle représente toute la logique du jeu, qui est donc proprement séparé de l’exploration de l’arbre.
get_score
Cette méthode nous donne le score de l’état de jeux actuel. On peut ainsi donner un gros score si on gagne, un score négatif si l’on perd, etc
C’est ici qu’on peut devenir un peu créatif : Pour AlphaGo, Google a utilisé des réseaux de neurones pour évaluer une situation, de mon côté, j’ai fait une simple grille d’occupation, mais on peut aussi se contenter de la somme des scores des pièces en jeu, ce que vous voulez vraiment !
Si notre jeu se joue à plusieurs, contre des adversaires, n’oubliez pas de renvoyer le score * -1.0 ou autre pour que notre arbre comprenne qu’un bon coup joué par un adversaire est un mauvais coup pour nous !
À vous de garder l’ordre de jeux en tête dans cette classe, notre arbre ne verra que des scores.
get_move_count
On renvoie le nombre de coups possibles après celui-ci (de 0 a l’infini).
Ce nombre sera utilisé comme index par notre exploration d’arbre : Si on lui dit qu’il a 3 coups possibles, il appellera la fonction membre do_move avec un index de 0 a 2.
Si cette fonction renvoi 0, cela signifie qu’aucun coup n’est jouable par la suite : on a fini d’explorer cette branche.
Pour cette fonction, je vous conseille de garder en mémoire (dans un vector par exemple) les coups possibles, pour ne les calculer qu’une seule fois.
Calculer les coups possibles dépend du jeu que vous avez choisi d’implémenter, bon courage donc.
do_move
Cette méthode est la plus importante : elle prend en entrée l’index d’un coup possible (entre 0 et get_move_count() - 1) et nous renvoie un nouveau game state qui correspond à l’état du jeu une fois ce coup joué.
Pas de soucis de désallocation, notre classe Node s’en occupera (même si l’utilisation d’un smart pointer aurait été à préférer)
Notre arbre
Enfin la partie intéressante ! On fait ici une classe Node, qui représente un nœud de l’arbre. Il est responsable du choix des enfants à créer, de comment explorer le bazar et de remonter les scores, puis nous dire quel est le meilleur combo.
class Node {
//creer la node depuis un etat de jeux
Node(Node* parent, IGame_State* gameState);
//trouve l enfant avec le meilleur score
Node* get_best_child_UCB ();
Node* get_best_child_UCT ();
//Ajoute un enfant parmi les coups possibles
Node* expand_children ();
//deroule une partie depuis cette node
float rollout ();
//remonte le score a la racine
void backpropagate (score);
private:
Node* _parent; //référence au parent
list<Node*> _children; //référence aux enfants
IGame_State* _state; //référence a l'état de jeu associé a cette node
double _score; //score a cette node
unsigned int _nombreDeVisites; //Nombre de passages par cette node
}
Notre class contient une référence à son parent dans un pointeur, pour l’étape de backpropagation.
J’utilise une list pour stocker les enfants, car on ne connait pas leur nombre. Utiliser un vecteur est également possible, mais ici, je n’ai jamais besoin d’accéder à un enfant par index, ils seront toujours choisis par itération. Utiliser une map où un tableau à taille variable (comme vector) n’est pas intéressant quand une liste simplement chainée suffit. Et oui, ce ne sont pas des smart pointers pour une raison de lisibilité (pas tant de place que ça sur un billet de blog).
Nous avons aussi un membre _state contenant l’état du jeu correspondant à cette node.
Elle ne peut contenir que des références vers une classe dérivée de notre interface IGame_State, dont nous utilisons les fonctions dans notre recherche.
Les membres _nombreDeVisites et _score contiennent respectivement le nombre de passages par cette node (uniquement en backpropagation) et le score associé a l’état de jeux _state et les scores de tous les enfants.
Du côté des méthodes, on a besoin de 4 méthodes de base pour MCTS. Élaborons un peu tout ça.
Constructeur
Notre constructeur prend une classe dérivée de notre interface IGame_State, qui correspond à l’état de jeu de cette node.
Il récupère aussi son parent pour l’étape de backpropagation.
Il va alors vérifier si on a atteins le bout de l’arbre, en appelant la méthode get_move_count () de notre game state, et vérifier s’il est égal à 0.
Si c’est le cas, la recherche dans cette branche est terminée, on peut appeler backpropagate () et faire un petit café pour fêter ça : une suite de coups terminée, une !
get_best_child
On appelle cette méthode lors de l’exploration, seulement quand notre node à des enfants.
Ça parait simple : trouver le meilleur des enfants et le renvoyer.
Mais comment on sélectionne le meilleur enfant ?
Si on utilise la fonction get_score, on va faire une recherche greedy sans exploration, on ne veut pas de ça.
Ça n’est pas non plus le moment de créer une euristique d’évaluation (quoi que si ça vous amuse…)
J’ai beaucoup vu sortir la formule UCB1 (Upper Confidence Bound 1), qui renvoi la somme des scores sur la somme des visites, qui permet de balancer l’exploration et les performances. $$ UCB1(visits, score) = \frac{score}{visits} $$
On va utiliser Une amélioration de cette méthode, appelé UCT (UCb1 applied to Trees), qui donne un contrôle sur l’exploration : $$ UCT(visits, score, parentVisits) = UCB1(visits, score) + c \sqrt{ \frac{ln(parentVisits)}{visits} } $$ Avec c un paramètre permettant de régler le “taux” d’exploration désiré (> 0).
Le principe est encore une fois assez simple : on additionne à l’UCB1 un nombre qui favorise l’exploration.
Le logarithme utilisé ici sur le nombre de visites du parent permet ici d’explorer en priorité les enfants les moins explorés (nombre de visites petit par rapport aux visites du parent). Le logarithme permet de diminuer l’exploration quand le nombre de visites augmente (ie: on converge vers une solution).
Ici, on voudra utiliser les deux métriques, on aura besoin :
- d’une fonction
get_best_child_UCTpour la phase d’exploration - d’une fonction
get_best_child_UCBpour sélectionner le meilleur coup final.
expand_children
Cette méthode choisie un coup à jouer parmi ceux proposés par le game state, et ajoute une node en enfant de notre node. L’adresse de ce nouvel enfant est renvoyée pour pouvoir lancer la phase rollout.
Pour créer un nouvel enfant, on va utilise la fonction do_move de notre interface IGame_State pour obtenir un nouvel état de jeu correspondant à l’état de l’enfant.
On peut ensuite appeler le constructeur de node avec cet état de jeu.
Node* Node::expand_children () {
unsigned int index = //choisir un index non exploré
//obtenir le prochain etat
IGame_State* nextState = _state->do_move(index);
//nouvelle node avec celle ci comme parent et le nouveau state
return new Node(this, nextState);
}
Pour le choix de l’index, on est tout à fait libre. C’est un bon endroit pour utiliser un peu d’aléatoire (pour commencer) et marquer sur notre CV qu’on a utilisé une recherche de Monte Carlo. On améliorera ça dans la partie 2.
rollout
Une de mes préférées ! C’est la phase “joue des coups jusqu’à ce que ça ne soit plus possible” de notre exploration.
L’appellation Monte Carlo désigne un choix aléatoire quelque part dans notre programme, et c’est généralement à cet endroit : On va choisir un coup possible au hasard depuis notre état actuel, et faire un coup possible depuis ce nouvel état et ainsi de suite. On récupère alors le score de l’état final qu’on renvoie.
J’ai vu assez souvent des gens qui oublient la partie Monte Carlo de l’exploration d’arbre avec Monte Carlo, mais on leur pardonne, après tout, on fait ce qu’on veut !
Pour s’amuser, on peut changer le choix aléatoire par un choix déterministe, et faire des choix greedy, ou inventer une euristique, liberté absolue de ce côté-là.
void Node::rollout() {
IGame_State* currentState = _state;
while(currentState->get_move_count() > 0) {
currentState = currentState->do_move(
//index a choisir
) );
}
//propager le score de l'état final
this->backpropagate(
currentState->get_score()
);
}
On n’utilise ici que des classes dérivées de IGame_State, aucune node n’est créée.
backpropagate
Une fois la phase de rollout terminée, on va remonter le score de notre node jusqu’à la racine. Elle ajoute le score au score de la node actuel, et on incrémente le compteur de visites.
Cette fonction est récursive : si on a un parent, on appelle _parent->backpropagate(score) après avoir changé nos scores et le tour est joué !
Quelque chose comme
void Node::backpropagate (score) {
//incremente le nombre de visites et score
_nombreDeVisites += 1;
_score += score;
if(dynamic_cast<Node*>(_parent) != nullptr) {
//propager au parent si il existe
_parent.backpropagate(score);
}
}
J’ai utilisé un dynamic_cast pour le test de l’existence du parent, ça peut sauver dans un cas où cette classe est utilisée comme base pour une nouvelle classe Node, crée par un programmeur négligent qui n’aurait pas pensé à faire _parent = nullptr dans le constructeur, ou une si on rencontre une désallocation sauvage du parent entre deux appels (oui oui les smart pointers…).
Faire fonctionner le tout
Il manque une étape, on a toute la logique, mais rien pour la lancer. Ça n’est pas bien compliqué maintenant, le gros du travail est fait.
Il reste cependant un aspect intéressant non abordé : décider de la limite. On ne va pas laisser cet algorithme tourner jusqu’à ce que le ciel nous tombe sur la tête, il nous faut décider d’une limite au-delà de laquelle on arrête nos itérations. Un simple compteur fera l’affaire (“cherche N solutions, et rappels moi quand t’as fini !”), mais une solution à peine plus élaborée sera de choisir une limite temporelle (“fais ton bazar pendant 5 secondes et zou”).
Node root(nullptr, gameState);
do {
//chercher la meilleure feuille
Node* child = root;
while(child->get_move_count() > 0) {
if(not child->is_fully_expanded() ) {
//all children have not been explored
child = child->expand_children();
break;
}
child = child->get_best_child_UCT();
}
if(child->get_move_count() != 0) {
//can expand
double score = child->rollout();
child->backpropagate(score);
}
} while (on a du temps);
IGame_State* bestMove = root->get_best_child_UCB(); //use UCB
Et voilà ! La structure de l’arbre est très basique, dans la partie 2 on va discuter améliorations !