Après m’être attaqué a la génération procédurale de systèmes planétaires, j’ai décidé de monter un peu dans l’échelle de l’univers en tentant ma chance sur les galaxies.
On cherche à respecter plusieurs conditions essentielles pour un observateur qui peut se trouver n’importe où dans la galaxie :
- Les étoiles brillantes doivent être vues de très loin.
- Les étoiles proches doivent être générée indépendamment de leur luminosité.
- Le modèle galactique doit exister pour chaque point de l’espace (x, y, z)
Définir la forme
Quand on dit “galaxie”, on pense généralement à une structure en spirale aplatie sur un plan, avec un noyau à son centre.
Dans notre univers, on repère bien sûr des formes plus diverses, parfois avec des spirales, spirales barrées, disque plein, boules, ou même des formes arbitraires (galaxies irrégulières). On va s’intéresser ici a la génération de galaxies spirales, qui sont à mon avis les plus jolies et celles dont la forme est la plus difficile à définir algorithmiquement. Plus particulièrement, je vais ici décrire le processus de génération des galaxies en spiral régulières.
J’ai choisi de me baser sur le papier A New Formula Describing the Scaffold Structure of Spiral Galaxies, qui présente une formule facilement paramétrable, qui décrit suffisamment bien les comportements qu’on retrouve dans la nature.
Elle est définie en coordonnées polaires par l’équation suivante : $$ r(\phi) = \frac{A}{ log(B \tan\frac{\phi}{2N}) } $$ Avec A un paramètre d’échelle, B et N des paramètres pour contrôler le degré de pente de la spirale.
Quelques exemples avec A fixé à 1 :
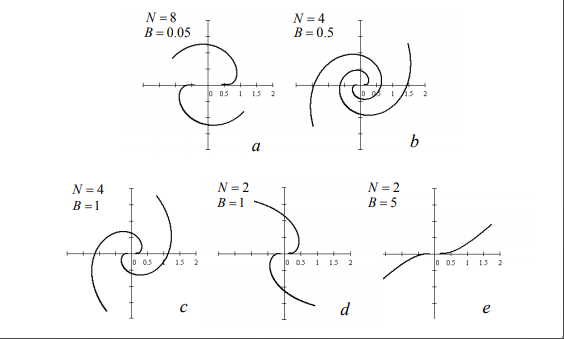
J’ai implémenté cette équation de façon à pouvoir l’utiliser par la suite comme une fonction de densité de l’espace : On prend un point (x, y, z) dans l’espace, on obtient la densité d’étoile en ce point.
Voilà une petite galaxie à deux bras :

Définir des densités
Une fois la forme de la galaxie définie, j’ai posé un algorithme général pour obtenir en chaque point de l’espace la probabilité d’y trouver une étoile :
Bulbe central
Le cœur de la galaxie est une simple équation de densité inverse. J’ai décidé d’utiliser la loi de Vancouleurs.
$$ d_{bulge}(r) = I_0 e^{-K r^{0.25} - 1} $$
Avec r la distance normalisée au centre de la galaxie (entre 0 et 1), K un paramètre permettant de contrôler la diminution de la densité du bulbe central (> 0), I0 un multiplicateur pour la valeur finale
Densité générale
Les bras sont également modélisés par une exponentielle inverse: $$ d_{arms}(r) = I_0 e^{-K Br^{0.25} - 1} * e^{-\frac{r - Br}{R_5} } $$
Avec Br le rayon normalisé du bulbe central (entre 0 et 1), et R5 la distance à partir de laquelle la densité passe sous 0.5.
On switch de l’équation 1 a l’équation 2 en fonction de notre distance au bulbe :
if (r < Br)
//use bulge density
else
//use arms density
Résultat de la loi de densité pour les paramètres I0 = 2, Br = 0.1, K = 0.2, R5 = 0.2, en fonction du rayon normalisé :
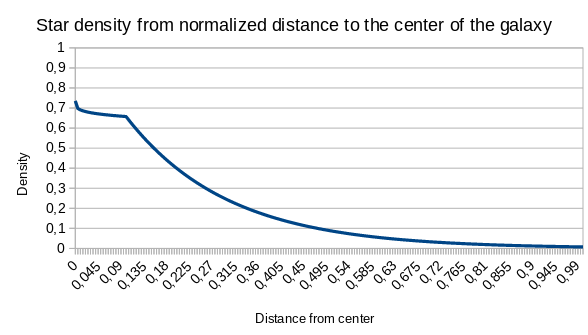
Cette équation peut décrire la densité d’étoiles dans une galaxie de n’importe quel forme, et il nous faut donc ajouter une formule de densité pour les bras .
Bras
$$ d_{from arms} = e^{-\frac{Da}{Ra}}. $$
Avec Da la distance au bras le plus proche et Ra le rayon (normalisé) d’un bras.
Et voilà les bras peuplés selon la loi de densité par 4000 étoiles.
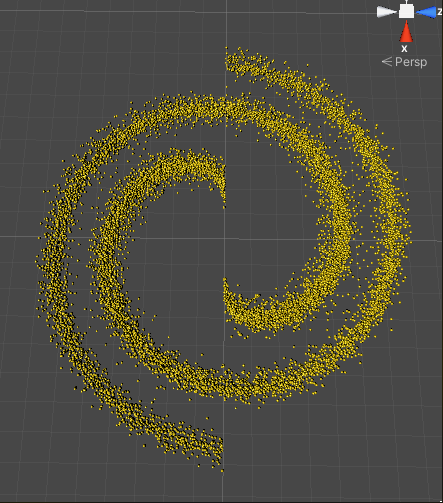
On observe que la densité est plus forte vers le centre de la galaxie ainsi qu’au centre des bras (le centre et la barre ne sont pas représentés).
400 milliards d’étoiles sans bruler la RAM
Dans notre chère Voie Lactée, on estime qu’on peut y trouver de 200 à 400 milliards d’étoiles. Les étoiles visibles (a l’œil nu) depuis la terre le sont surtout en fonction de leur luminosité et proximité. On peut en effet s’attendre à ce que des étoiles très lumineuses soient visibles de très loin, et que des étoiles très proches soient également visibles malgré leur faible luminosité
Cependant, les étoiles les plus lumineuses sont également les plus rares (classe O et B), tandis que les plus nombreuses et également les plus proches sont les moins lumineuses (classe M, K). Afin de ne pas générer les milliards d’étoiles de notre galaxie en mémoire et faire exploser mon ordinateur, il serait plus intelligent de ne générer que les étoiles visibles depuis notre point d’observation.
En m’inspirant du développement d’Elite Dangerous et du Journal de Ysaneya, j’ai décidé de mettre en place un octree (en gros la structure 3D d’un arbre binaire), séparant ma galaxie en 8 cubes principaux, également subdivisibles jusqu’à une certaine échelle. Les cubes les plus grands sont placés au “niveau 0”, jusqu’aux plus petits au “niveau 12” (Elite Dangerous utilise 8 niveaux).
L’observateur se situe dans un cube de niveau 12, c’est-à-dire dans un cube occupant 1/4096 ème de la galaxie. Pour la voie lactée, ça représenterait un cube de 126.9 x 126.9 x 126.9 années-lumière, assez pour contenir le soleil et son voisinage proche, ce qui représente un nombre considérable d’étoiles (voir un exemple du voisinage à 250 années lumières du soleil).
Image de l’octree subdivisé jusqu’au niveau 12, avec quelques étoiles réparties avec une loi de densité uniforme.
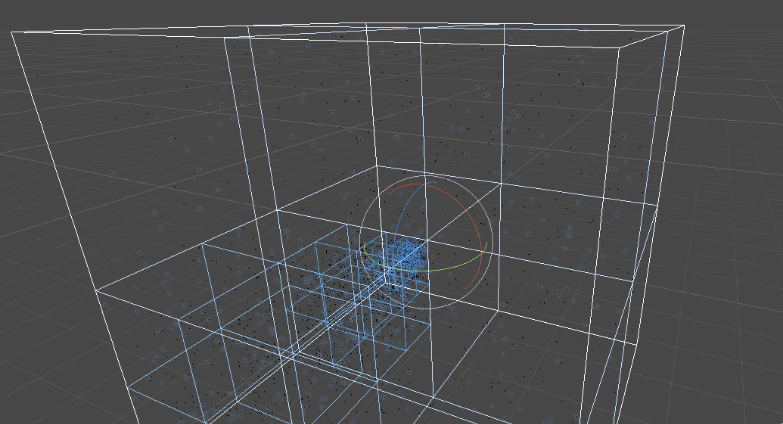 On peut voir que même avec une répartition uniforme, les étoiles sont affichées en plus grand nombre autour de l’observateur.
On peut voir que même avec une répartition uniforme, les étoiles sont affichées en plus grand nombre autour de l’observateur.
Chaque niveau de cet octree possède une probabilité d’apparition des étoiles : les niveaux les plus bas (0-3) favorisent l’apparition des étoiles très lumineuses, visibles de très loin mais dont l’apparition dans l’univers est assez rare (1-2%). Les niveaux intermédiaires (4-9) gèrent l’apparition d’étoiles intermédiaires, moins lumineuses que les O et B, mais également bien plus nombreuses. Les derniers niveaux s’occupent des étoiles peu lumineuses, mais très courantes, comme les naines jaunes, oranges et rouges. Le tout dernier niveau peut aussi s’occuper des cas particuliers, comme les naines blanches et les étoiles ratées (classe K, J, …).
On génère donc les étoiles lumineuses très éloignées de l’observateur, tout en garantissant que les étoiles proches, mais peu lumineuses soient visibles.
Je n’ai pas encore envisagé de solution fiable pour l’apparition des trous noirs et des nébuleuses. Je cherche en ce moment une méthode pour rendre les coefficients d’apparition des étoiles par niveau de l’octree plus “procéduraux” que de les rentrer à la main, afin de faire apparaitre des résultats plus diversifiés et intéressants.