Part 1: Blabla and Implementation
I’m terrible at chess, checkers, get rolled over in Connect 4 – in short, board games are not my strong suit. However, I do fairly well in programming.
A quick note: from here on, when I say “sequence of moves,” I mean a turn order: I play, then my opponent, then me, and so on.
Skip the blabla and jump to the interesting part.
Imagine Yourself Playing Chess
What strategy to adopt? One might think of keeping it simple and playing pawns randomly, but the probability of winning is quite low if your opponent doesn’t have the same strategy (unless you pretend to know what you’re doing, which can unsettle them). Let’s call this the “random method.”
The next step would be to choose completely random moves and keep the best one in mind until your opponent announces, “Well, you haven’t moved your pawn in an hour, I’m out” (victory!) or, if you’re playing with an hourglass, your defeat. This approach is much better than playing random moves directly since your final solution depends on all previous moves. However, in these types of games, the number of possible moves increases exponentially, making it impossible to try them all (well, possible but not under the pressure of the hourglass!). Let’s call this the “exploration method.”
Or another method would be to think only about the best moves you can make, then the best moves you can make after those best moves, and so on. This kind of method is called greedy, meaning it makes decisions on the spot without time to think about the sequence of events! This approach is already better than the previous two because it explores fewer possibilities (less headache!) and performs a series of actions that are inherently positive (for a result not necessarily as positive). Its disadvantage is easily falling into local minima, like jumping your queen onto a knight to have it taken by a pawn. Similarly, it will never sacrifice a pawn to eat another more dangerous one, making its strategy very predictable. Let’s call this one the “greedy method.”
What we need is a method capable of bringing together the strengths of its friends, a kind of Captain Planet for board games! Fortunately, this problem has been thoroughly examined by intelligent people (and/or paid for it), who have found a set of solutions, each more original than the other. But here, we’re not aiming for originality, and we’ll only talk about trees, shall we?
Building a Tree
If you’ve ever dabbled in object-oriented programming, you’ve likely encountered this type of exercise. A tree is a fairly basic data structure where we have a set of nodes that belong to a parent and have children, who, in turn, have children, and so on. It’s a fairly intuitive representation for us, poor monkeys, and we find it everywhere, in all application domains (see my little post on procedural galaxy generation, where the galaxy is created in a tree).
Here, our root will be the basic position of the board, with no moves if I start, or with a move from the opponent if they start (fewer moves to calculate, yes!). Each possible move from the initial situation will represent a new child for our root. Then, once we’ve explored all our moves, it’s the opponent’s turn. We generate their possible moves from each of our moves, then it’s my turn, and so on until we reach the end of the game (win, lose, draw, who knows).
A small example with Tic-Tac-Toe:
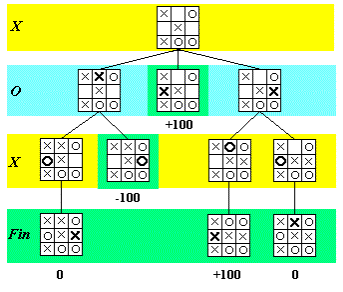(Borrowed from the turing.cs website, worth visiting for explanations of more varied algorithms)
Alright, now we have a tree.
Exploration with Monte Carlo
The tree we just built is of a reasonable size for Tic-Tac-Toe, where the number of possibilities is limited. For Connect 4, it could still work, but for chess (or Go), it’s not viable. There are several techniques to improve all this, the one that interests us is called MCTS “Monte Carlo Tree Search” (see the Wikipedia page, which talks less than me).
This technique was used as the basis for the AlphaGo algorithm, the world champion of the game of Go in 2015 (feeling old). It is based on some heuristics to find a balance between exploring new possibilities and searching around the best action sequences already found. This allows exploring only a fraction of the possibilities while finding interesting moves.
The purpose of this blog post is not to provide a history or explain once again this method on the internet but to propose some modifications.
A quick summary to be on the same page: the difficulty of the technique consists of 4 steps:
- Traverse the tree with heuristics until reaching a leaf (a node without children).
- Create children for it: basically, add to it all possible moves from this node.
- Play random moves from the child created just before until reaching a final state.
- Propagate the final score from the child to the root.
Representing This in Code
We’ll create a very simple generic class for the tree, which will be responsible for choosing possible moves, carrying them out to the end, and propagating the result. The goal is not to provide code but simply the overall structure and details of a few methods.
Interface Game State
We need to code the game’s logic. For that, feel free to do what you want! The only constraint is that your game logic class should inherit from our interface below:
// Interface
class IGame_State {
// Return the score of this state
virtual double get_score() = 0;
// Return the number of possible moves from this state
virtual int get_move_count() = 0;
// Perform a move from this state and return it
virtual IGame_State* do_move(unsigned int index) = 0;
}
Our derived class IGame_State will be used in our tree to know where we are in the game. It represents all the game logic, which is neatly separated from tree exploration.
get_score
This method gives us the score of the current game state. You can assign a high score if you win, a negative score if you lose, etc.
This is where you can get a bit creative: For AlphaGo, Google used neural networks to evaluate a situation; on my end, I made a simple occupancy grid, but you can also settle for the sum of the scores of the pieces in play, whatever you prefer!
If your game involves multiple players, against opponents, don’t forget to return the score * -1.0 or another appropriate value so that our tree understands that a good move played by an opponent is a bad move for us! Keep the turn order in mind in this class; our tree will only see scores.
get_move_count
We return the number of possible moves after the current one (from 0 to infinity). This number will be used as an index by our tree exploration: if we tell it that it has 3 possible moves, it will call the member function do_move with an index from 0 to 2. If this function returns 0, it means no move is playable afterward: we’ve finished exploring this branch.
For this function, I recommend keeping track of possible moves (in a vector, for example) to calculate them only once.
Calculating possible moves depends on the game you have chosen to implement, so good luck.
do_move
This method is the most important: it takes the index of a possible move (between 0 and get_move_count() - 1) and returns a new game state that corresponds to the game state once this move is played.
No worries about deallocation; our Node class will take care of it (although using a smart pointer would have been preferable).
Our Tree
Finally, the interesting part! Here, we create a Node class, representing a node in the tree. It is responsible for choosing which children to create, how to explore the mess, and how to propagate scores, then tell us what the best combo is.
class Node {
//create the node from a game state
Node(Node* parent, IGame_State* gameState);
//find the child with the best score
Node* get_best_child_UCB();
Node* get_best_child_UCT();
//Add a child among the possible moves
Node* expand_children();
//play a game from this node
float rollout();
//propagate the score to the root
void backpropagate(score);
private:
Node* _parent; //reference to the parent
list<Node*> _children; //reference to the children
IGame_State* _state; //reference to the game state associated with this node
double _score; //score at this node
unsigned int _visitCount; //Number of visits to this node
}
Our class contains a reference to its parent in a pointer, for the backpropagation step.
I use a list to store the children because we don’t know their number. Using a vector is also possible, but here, I never need to access a child by index; they will always be chosen by iteration. Using a map or a dynamically sized array (like a vector) is not interesting when a simple linked list is sufficient. And yes, these are not smart pointers for readability reasons (there’s not that much space on a blog post).
We also have a _state member containing the game state corresponding to this node. It can only contain references to a class derived from our IGame_State interface, whose functions we use in our search.
The _visitCount and _score members respectively contain the number of passes through this node (only in backpropagation) and the score associated with the game state _state and the scores of all the children.
Regarding the methods, we need 4 basic methods for MCTS. Let’s elaborate on all of this.
Constructor
Our constructor takes a class derived from our IGame_State interface, which corresponds to the game state of this node. It also retrieves its parent for the backpropagation step.
It will then check if we have reached the end of the tree, by calling the get_move_count() method of our game state, and checking if it is equal to 0.
If so, the search in this branch is complete; we can call backpropagate() and make a little coffee to celebrate: a sequence of moves completed!
get_best_child
We call this method during exploration, only when our node has children.
It seems simple: find the best child and return it.
But how do we select the best child? If we use the get_score function, we’ll perform a greedy search without exploration, and we don’t want that. Now is not the time to create an evaluation heuristic (although, if it amuses you…).
I’ve often seen the UCB1 formula (Upper Confidence Bound 1) come up, which returns the sum of scores over the sum of visits, balancing exploration and performance. $$ UCB1(visits, score) = \frac{score}{visits} $$
We’ll use an improvement of this method called UCT (UCb1 applied to Trees), which provides control over exploration: $$ UCT(visits, score, parentVisits) = UCB1(visits, score) + c \sqrt{ \frac{ln(parentVisits)}{visits} } $$ With c a parameter allowing you to adjust the desired “rate” of exploration (> 0).
The principle is once again quite simple: we add to UCB1 a number that favors exploration.
The logarithm used here on the parent’s visit count allows us to prioritize exploring the least explored children (number of visits small compared to the parent’s visits). The logarithm helps decrease exploration as the visit count increases (i.e., converging toward a solution).
Here, we’ll want to use both metrics. We’ll need:
- a function
get_best_child_UCTfor the exploration phase - a function
get_best_child_UCBto select the final best move.
expand_children
This method chooses a move to play from those proposed by the game state and adds a node as a child to our node. The address of this new child is returned to be able to initiate the rollout phase.
To create a new child, we use the do_move function of our IGame_State interface to get a new game state corresponding to the child’s state. We can then call the node constructor with this game state.
Node* Node::expand_children() {
unsigned int index = //choose an unexplored index
//get the next state
IGame_State* nextState = _state->do_move(index);
//new node with this one as the parent and the new state
return new Node(this, nextState);
}
For the choice of the index, you are entirely free. It’s a good place to use a bit of randomness (for starters) and mark on your CV that you used a Monte Carlo search. We’ll improve this in part 2.
rollout
One of my favorites! It’s the “play moves until it’s no longer possible” phase of our exploration.
The term Monte Carlo designates a random choice somewhere in our program, and it’s usually at this point: we choose a possible move at random from our current state and make a possible move from this new state, and so on. We then retrieve the score of the final state and return it.
I’ve often seen people forget the Monte Carlo part of tree exploration with Monte Carlo, but we forgive them; after all, we do what we want!
For fun, you can change the random choice to a deterministic choice, make greedy choices, or invent a heuristic—absolute freedom on that side.
void Node::rollout() {
IGame_State* currentState = _state;
while (currentState->get_move_count() > 0) {
currentState = currentState->do_move(
//index to choose
));
}
//propagate the score of the final state
this->backpropagate(
currentState->get_score()
);
}
Here, we only use classes derived from IGame_State; no nodes are created.
backpropagate
Once the rollout phase is complete, we’ll propagate the score of our node up to the root. It adds the score to the current node’s score, and we increment the visit counter.
This function is recursive: if we have a parent, we call _parent->backpropagate(score) after changing our scores, and we’re done!
Something like
void Node::backpropagate(score) {
//increment the visit count and score
_visitCount += 1;
_score += score;
if (dynamic_cast<Node*>(_parent) != nullptr) {
//propagate to the parent if it exists
_parent.backpropagate(score);
}
}
I used a dynamic_cast for testing the existence of the parent; it can save you in a case where this class is used as the base for a new Node class, created by a negligent programmer who didn’t think to do _parent = nullptr in the constructor, or if we encounter wild deallocation of the parent between two calls (yes, yes, smart pointers…).
Making It Work
One step is missing; we have all the logic but nothing to launch it. It’s not too complicated now; most of the work is done.
However, there’s an interesting aspect not covered: deciding the limit. We won’t let this algorithm run until the sky falls on our heads; we need to decide on a limit beyond which we stop our iterations. A simple counter will do the trick (“look for N solutions and remind me when you’re done!”), but a slightly more elaborate solution is to choose a time limit (“do your thing for 5 seconds, and off you go”).
Node root(nullptr, gameState);
do {
//search for the best leaf
Node* child = root;
while (child->get_move_count() > 0) {
if (not child->is_fully_expanded()) {
//all children have not been explored
child = child->expand_children();
break;
}
child = child->get_best_child_UCT();
}
if (child->get_move_count() != 0) {
//can expand
double score = child->rollout();
child->backpropagate(score);
}
} while (we have time);
IGame_State* bestMove = root->get_best_child_UCB(); //use UCB
And there you have it! The tree structure is very basic; in part 2, we’ll discuss improvements!